Principles behind the TIR100
Measuring principle
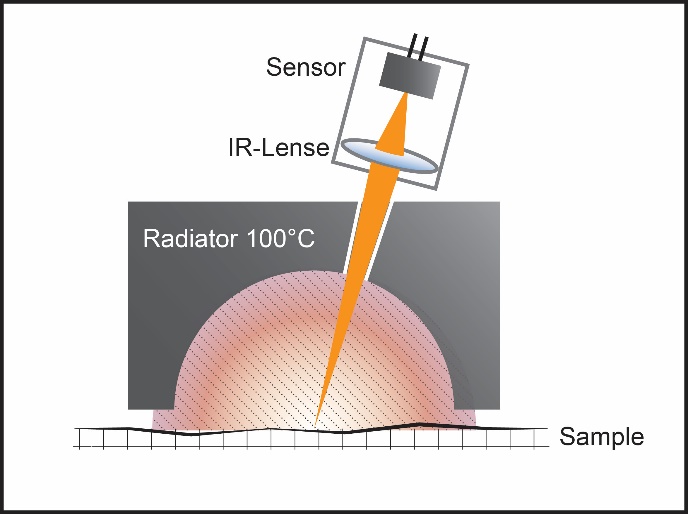
The sample is subject to thermal radiation at a temperature of 100°C. A black body half-sphere radiator is used to capsulate the sample to ensure homogenous illumination. The reflected infrared radiation is observed at an angle and is converted into a numeric value. This value is then plotted against a calibration table from high and low emissivity reference standards.
All of this is accomplished at a touch of a button when using the TIR.
Specifications of the TIR100-2
| Voltage range | 90 VAC – 260 VAC |
|---|---|
| Power rating | 240 VAC max. 130 W 120 VAC max. 260 W |
| Measuring range | As Calibration Standards |
| Measure Uncertainty | +- 0,005 (lowE) … +-0,01 (hiE) |
| Spectral range | 2,5 – 40µm |
| λmax of radiant energy | 7,8 µm |
| Radiator temperature | 100°C |
| Measuring Duration | approx. 5 sec. |
| Measuring spot | approx. 5mm |
| Interface | USB-B |
| Dimension | 230mm x 140mm x 120mm |
| Weight | TIR100-2: approx. 2,0kg |
Some basic physics principles
Stefan Boltzmann‘s law
The following physic principles are used to determine the emissivity from a black body radiator.
Every body with a temperature above absolute zero radiates thermal heat. The quantity of heat (power) is given by
P= σ * ε * T4
P = RadiativePower [W/㎡]
T=Temperature[K]
ε = Emissivity
σ = Planck’s Constant [W/K4㎡]
Emissivity ε is the degree of radiative energy compared to that of an ideal blackbody:
ε = 0 .. 1
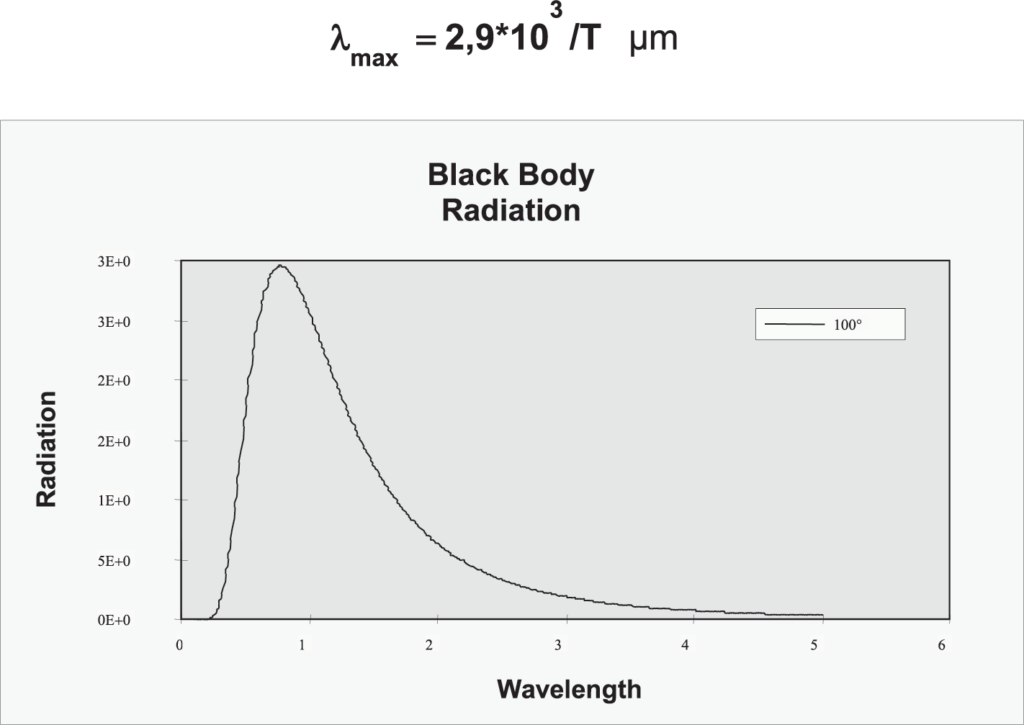
WIEN’S DISPLACEMENT LAW
Wien’s displacement law states that the wavelength distribution of radiated heat energy from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced, or moved over, on the graph.
The wavelength of maximum radiative energy could be calculated by
Principles of emissivity measurement



Some TIR100 principles
Based on the following principles, the TIR100 can give a numeric value
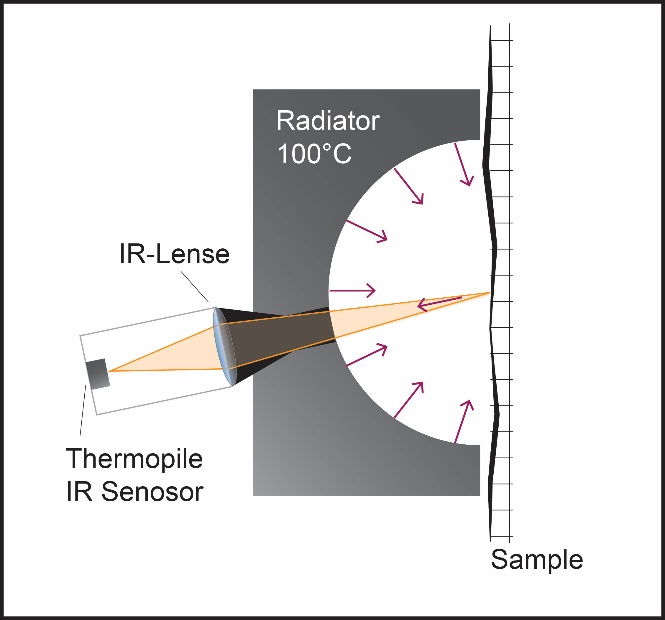
Measurement of reflected energy of a 100°C blackbody with hemispherical radiator
Black body power:
Pb = ε x σ x T4 (ε ~ 1)
Reflected power:
Pr = r x Pb
Emissivity:
ε = 1 – r
Some mathematical principles
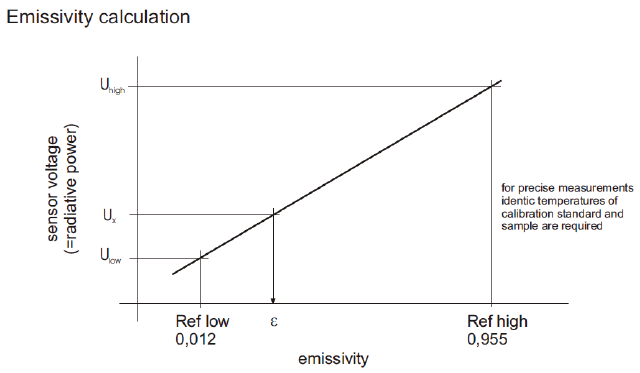
Based on the linear equation below, the TIR100 can calculate an emissivity value of a sample